Work, Energy & Momentum Flashcards
From conservation of energy to totally inelastic collisions, use these cards to master the topic of Work, Energy, and Momentum as tested in most introductory undergrad physics courses and even on the AP Physics exam. (86 cards)
What is the work done by a force F which acts on an object as it moves through a distance d?
W = F*d cos(θ)
Where θ is the angle between the force and the direction of motion.
Since work is proportional to cos(θ), only the component of force parallel to the motion contributes to the work; any forces perpendicular to motion do no work since cos(90)=0.
What are the units of work, as defined in physics?
Work has units of Joules (J).
Remember: work is defined as F * d cos(θ), which has units of N * m, or kg * m2/s2, which is identical to the units of Joules.
What is the sign of work done on an object if it begins at rest and an applied force accelerates in the same direction as the displacement of the object?
The work done on the object by the force is positive (+).
By definition, work done by a force that leads to a change in distance (hence an increase in speed) is positive work if it accelrates in the same direction as the displacement of the object.
If the force has a component in the direction opposite to the displacement, the force does negative work.
What is the sign of work done on an object, if it begins at speed v and an applied force decelerates it to rest?
The work done on the object by the force is negative (-).
By definition, work done by a force (such as friction) that leads to a decrease in speed is negative work.
What kind of work, positive or negative, can a person do by pushing on a box?
A person can do either positive or negative work by pushing on a box.
If the person pushes on the box in the same direction that it moves, then positive work is done. If the person pushes in the opposite direction of the moving box, then negative work is done.
What kind of work (positive, negative, or both) can frictional forces do?
Frictional forces can only do negative work.
By definition, frictional forces are always in the opposite direction of an object’s motion. Hence, they can only slow the object down, and only do negative work.
What is the work done by gravity as an object of mass m moves from the ground to a height h?
W = mgh
Remember, W = F * d cos(θ). In this case, as an object moves straight up, θ = 0º and cos(θ) = 1. So, W = F * d. The force of gravity is simply mg, and the distance is h, so the total work done is mgh.
An object at rest is moved from the ground to a height h/2, then to rest at a height h. How much work does gravity do during this process?
W = -mgh
The work done by gravity while the object moves to h/2 is -mg(h/2). The work done while the object is moving from h/2 to h is also -mg(h/2). Work is negative in this case, because gravity works against the object being moved.
Notice that this is identical to the work done if the object is moved directly to h; the work done by gravity is path-independent.
Define:
mechanical advantage
Mechanical advantage is the multiplication of a force using a mechanical device. A small force exerted over a large distance is transformed into a larger force over a smaller distance.
On the AP exam, mechanical advantage appears primarily in problems including levers.
What is the relationship between force and distance in any system which includes mechanical advantage?
F1d1 = F2d2
In any system exhibiting mechanical advantage, the force exerted and the distance covered are inversely proportional,
A force F1 is exerted a distance d1 from the fulcrum of a lever. What does the force F2 at d2 from the other end equal?
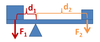
F2 = F1d1/d2
In any system exhibiting mechanical advantage, the force exerted and the distance are inversely proportional, F1d1 = F2d2. Rearranging yields the above relationship.
A pulley system is set up that allows a weight m to be lifted using a force of only (1/3)mg. How far must the string on which the force is exerted be pulled in order to move the weight a distance d?
The string must be pulled a distance 3d.
In any system exhibiting mechanical advantage, the force exerted and the distance are inversely proportional, F1d1 = F2d2. So if one-third of the force is required, the distance must increase by the same proportion.
Define:
power, as used in physics
Power is a measure of the rate of energy flow.
Power is defined as energy divided by time:
P = E/t
The units of power are Watts, where 1 W = 1 J/s.
What is the power flowing through a wire, if 1,000 J of energy flow through in 0.1 s.
P = 10,000 W = 10 kW
Power is energy divided by time;
1000 J / 0.1 s = 10,000 W
Note that kW is a commonly-used unit on the AP exam.
Define:
the kinetic energy of an object
An object’s kinetic energy is the energy resulting from its motion.
Kinetic energy is defined as:
KE = ½mv2
where m is the object’s mass and v is its speed. The units of kinetic energy are Joules, just like all other forms of energy.
If objects 1 and 2 are moving at the same speed, but object 2 has twice the mass of object 1, how do their kinetic energies compare?
KE2 = 2*KE1
Kinetic energy is defined as ½mv2, so it is directly proportional to the mass. If the objects’ speeds are the same, kinetic energy will increase proportionally with the mass.
If objects 1 and 2 are the same mass, but object 2 is moving at twice the speed of object 1, how do their kinetic energies compare?
KE2 = 4*KE1
Kinetic energy is defined as ½mv2, so it is directly proportional to the square of the velocity. If the objects’ masses are the same, kinetic energy will increase with the square of the velocity.
Define:
the work-energy theorem
The work-energy theorem states that the net work done on an object by all the forces acting on it equals the change in the object’s kinetic energy.
Wnet = ΔKE
An object is at rest, and a person pushes on it, doing 50 J of work that convert to motion. What is the object’s final kinetic energy? (assume no dissipative forces)
The object’s final KE is 50 J.
According to the work-energy theorem, the net work done on the object results in a change in its kinetic energy. Since the person is exerting the only force on the object which causes motion, the work done equals the change in kinetic energy.
An object is moving with 100 J of kinetic energy, and a frictional force acts on it, doing 50 J of work. What is the object’s final kinetic energy?
The object’s final KE is 50 J.
According to the work-energy theorem, the net work done on the object results in a change in its kinetic energy. Since the frictional force is the only force affecting motion, the work done equals the change in kinetic energy. Frictional forces can only do negative work, so the final kinetic energy is lowered.
An object with mass m falls through a distance h. What is its final kinetic energy? (assume no dissipative forces)
The object’s final KE is mgh.
According to the work-energy theorem, the net work done on the object results in a change in its kinetic energy. Since gravity is the only force acting on the object, the change in kinetic energy simply equals the work done. Work = F * d, or, in this case, mg * h. You might also recognize this as the gravitational potential energy of the object before it fell.
Define:
the gravitational potential energy of an object in a gravitational field
An object’s gravitational potential energy Ugr is defined as the work that was needed to raise it to its present height above an arbitrary reference point.
On the AP exam, the reference point will always be ground level, unless otherwise stated.
What is its gravitational potential energy of an object of mass m that is a height h above the surface of the Earth?
Ugr = mgh
This is identical to the work needed to raise the object that height, and is also equal to the kinetic energy the object will gain if it is allowed to fall freely to the ground.
How does the gravitational potential energy of a mass change, if its height above the surface of the Earth doubles?
The gravitational potential energy of the mass doubles.
Since gravitational potential energy of an object near Earth’s surface Ugr = mgh is proportional to height above the ground, changing the height changes the energy by the same amount.





















